Dennis, Elliot Cramer gave the standard error of r as [(1/n)* (1 - rho^2)^2]. For rho = .80, and n = 100, this would come to .036. The attached jpeg file is the result of bootstrapping 10,000 resamples from a data set where r = .801. You will see that the standard error there, which is simply the st. dev. of those 10,000 r's, is also .036, as it should be. Note that the 95% confidence limits are .718 and .862, which are asymmetric, as they should be. If we naively took r +/- 1.984(.036) we would get .730 and .872, which are symmetric, but wrong. Notice that the bootstrap distribution looks just like the textbooks say it should. Dave Howell________________________________________________________________
----------------------------------------------------------------------------------------------------------------
David C. Howell
Dept of Psychology
University of Vermont
Burlington, VT 05405
http://www.uvm.edu/~dhowell/StatPages/StatHomePage.html
http://www.uvm.edu/~dhowell/gradstat/index.html
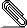 bootstrapCorr.jpeg
bootstrapCorr.jpeg